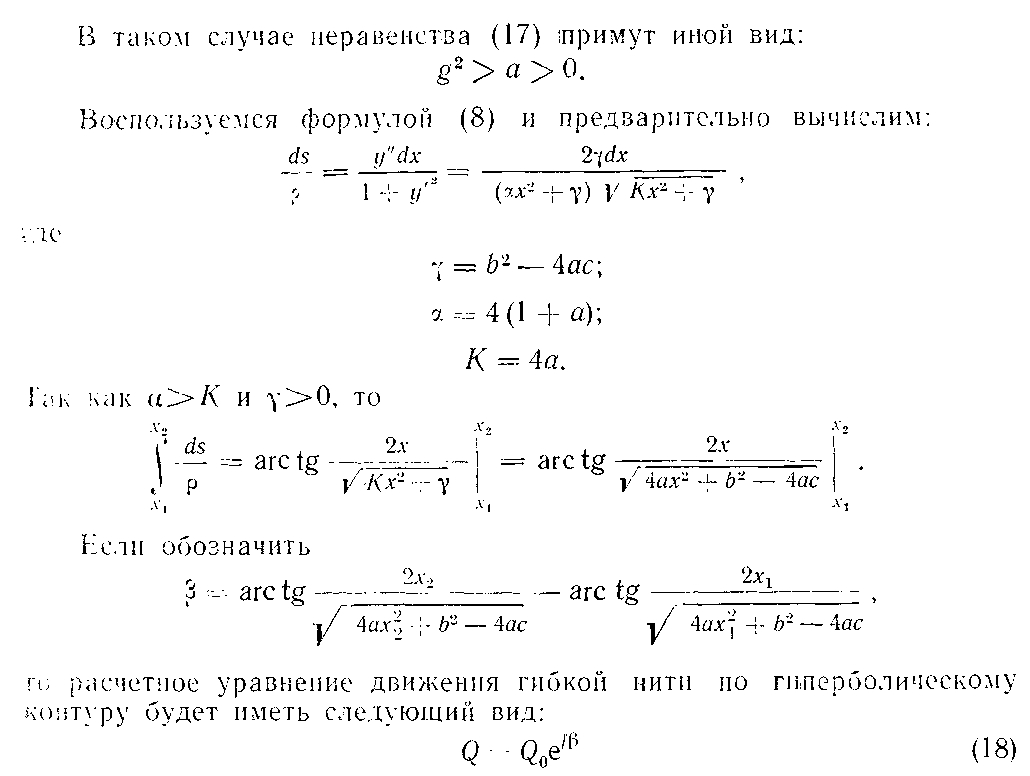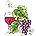Формулы (6—9) выведены при самой общей постановке вопроса, поэтому при использовании их в процессе расчетов реальных сельскохозяйственных машин требуется четкая конкретизация основных исходных положений.
Во-первых, необходимо установить, какому закону подчиняются силы трения в местах фрикционного контакта нити с направляющими контурами.
Во-вторых, следует выяснить, считать ли рассматриваемые нити невесомыми, или же отнести их к тяжелым гибким телам.
В-третьих, нужно задаться определенной формой нитепроводящих контуров.
Специальными исследованиями и расчетами ,в первую очередь была проведена оценка контурной площади контакта подвязочных нитей (шпагатов) с нитепроводящими деталями вязальных аппаратов сельскохозяйственных машин, так как на основании такой оценки можно довольно точно определять закон сил трения в местах соприкосновения трущихся материалов.
Для исследований применен метод Н. В. Хвальковского [5]. Из полученных при этом графических зависимостей площади контакта подвязочных нитей от их натяжения следует, что движенце нитей в вязальных аппаратах сельскохозяйственных машин осуществляется при наличии фрикционного контакта, находящегося в пластическом состоянии. Согласно исследованиям И. В. Крагельского [2], можно заключили, что силы трения в местах взаимодействия подвязочных нитей с нитепроводящими устройствами вязальных аппаратов приближенно подчиняются закону Амонтона, т. е.
Τ = fΝ, (10)
гдe Т сила трения;
А -нормальная нагрузка на контакт;
f- коэффициент трения по Амонтону.
Оценка влияния веса подвязочных нитей на точность расчетных формул была произведена теоретическим путем. Для упрощения вычислений использовали формулы Эйлера и А. П. Минакова. [4], выведенные для случая плоского равномерного движения гибких нитей по цилиндрическим поверхностям при наличии амонтонова трения. При этом считалось, что в качестве подвязочных нитей применяются шпагат сноповязальный и шпагат бумажный № 4.
Выполненные расчеты показали, что при скоростях движения, не превышающих 15 м. сек, собственным весом подвязочных нитей можно пренебречь (ошибка не превышает 1,5%) и считать их невесомыми.
Для определения наиболее распространенных форм нитепроводящих контуров были обследованы нитенаправляющие и нитенатяжные устройства следующих сельскохозяйственных машин: льнотеребилки ЛТВ-4, льнокомбайна ЛК-7, пресс-подборщика ППБ-1,3 матовязальных МШ-5 и МВМ-250, экспериментальных для подвязки винограда МЗП-1 и МЗПА-2. С интересующих нас деталей были сняты пластилиновые отпечатки. При последующей камеральной обработке собранные опечатки рассекались ножом в тех местах, где движется подвязочная нить. Получившиеся при этом плоские сечения и представляли собой нитепроводящие контуры.
Методами математической статистики для этих контуров были получены эмпирические формулы. Анализ этих формул показал, что ими описываются симметричные криволинейные контуры определенного типа - окружность, эллипс, парабола, гипербола. Ниже приводится характеристика нитепроводящих контуров по отдельным сельскохозяйственным машинам.
Окружность....................................................................... ЛТВ-4,... ЛК-7, ППБ-1,3,
МВМ-250, МЗП-1, МШ-5
Эллипс ................................................. ЛТВ-4, ЛК-7, ППБ-1,3;
МШ-5
Парабола .......................................................................... ЛТВ-4,... ЛК-7, ППБ-1,3,
МВМ-250, МЗП-1, ΜЗПА-2
Гипербола......................................................................... ЛТВ-4,... ЛК-7, МЗП-1,
ППБ-1,3
Таким образом, задача дальнейших исследований сводится к расчету невесомых гибких нитей, движущихся по плоским криволинейным контурам заданной формы, при условии, что силы трения в местах фрикционного контакта нити приближенно подчиняются закону Амонтона. Решение такой задачи будем проводить отдельно для каждого из типовых нитепроводящих контуров, используя формулы (8) и (9).
Движение гибкой нити по эллиптическому контуру

Движение гибкой нити по параболическому контуру
Так как задать уравнение параболы в параметрическом виде нс представляется возможным, напишем это уравнение в явном виде (рис. 4).
![]() (14)
(14)
где В -высота параболы;
а - некоторый размерный коэффициент (а>0).
Ширина основания параболы А выражается через В и а следующим образом:
![]()
Для расчетов воспользуемся формулой (8). Предварительно вычислим
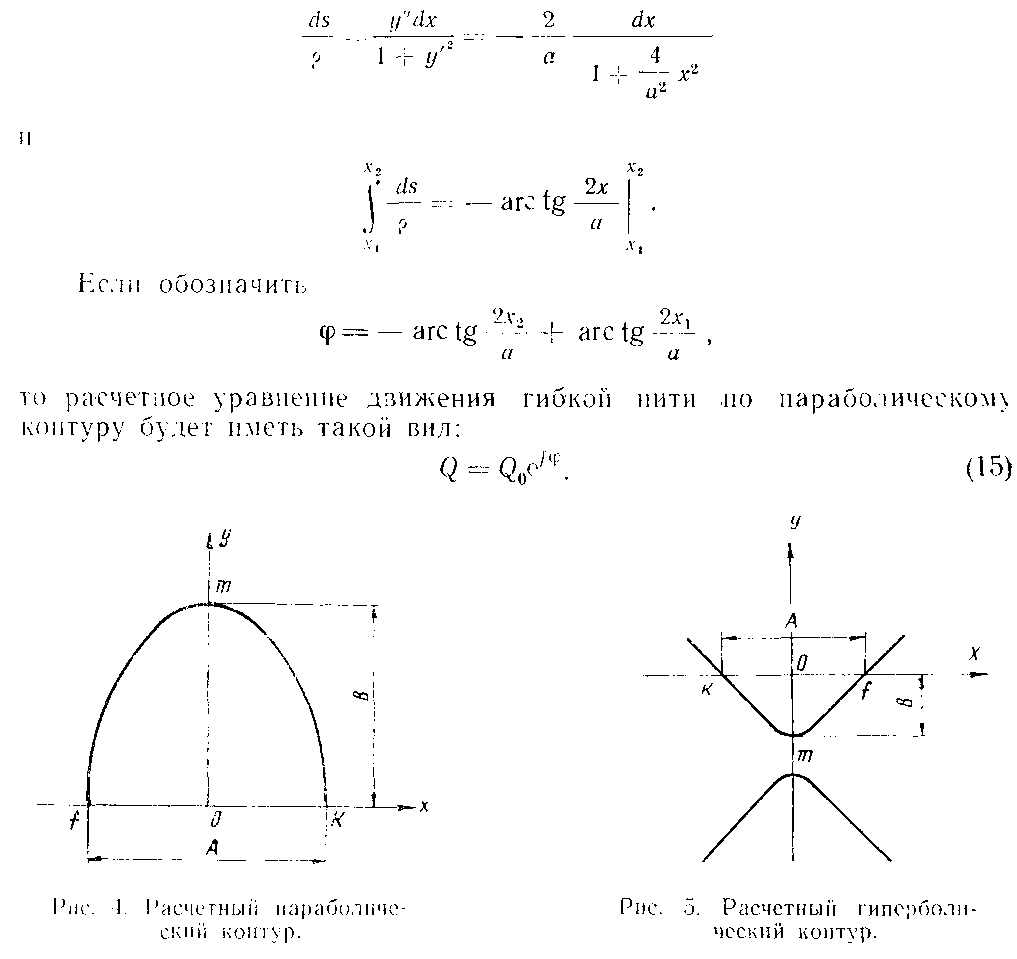
Движение гибкой нити по гиперболическому контуру
Для наших расчетов достаточно рассмотреть только верхнюю ветвь гиперболы на участке kmf, отсекаемом осью ОХ (рис. 5).
Зададим уравнение этой ветви в явном виде:

Если принять, что высота рассматриваемой части гиперболы От=В, ширина ее основания по оси ОХ равна А и между А и В существует такая зависимость А=2gВ, то размерные коэффициенты b и с в уравнении (16) будут выражаться таким образом:
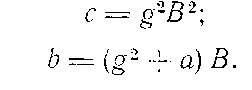
Коэффициент а является безразмерным параметром, характеризующим форму гиперболы.
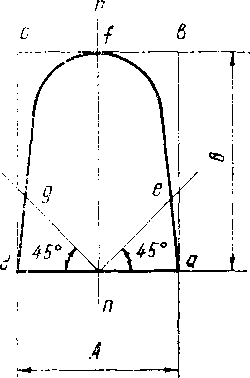
Рис. 6. Геометрическая модель нефтепровод ящего его контура.