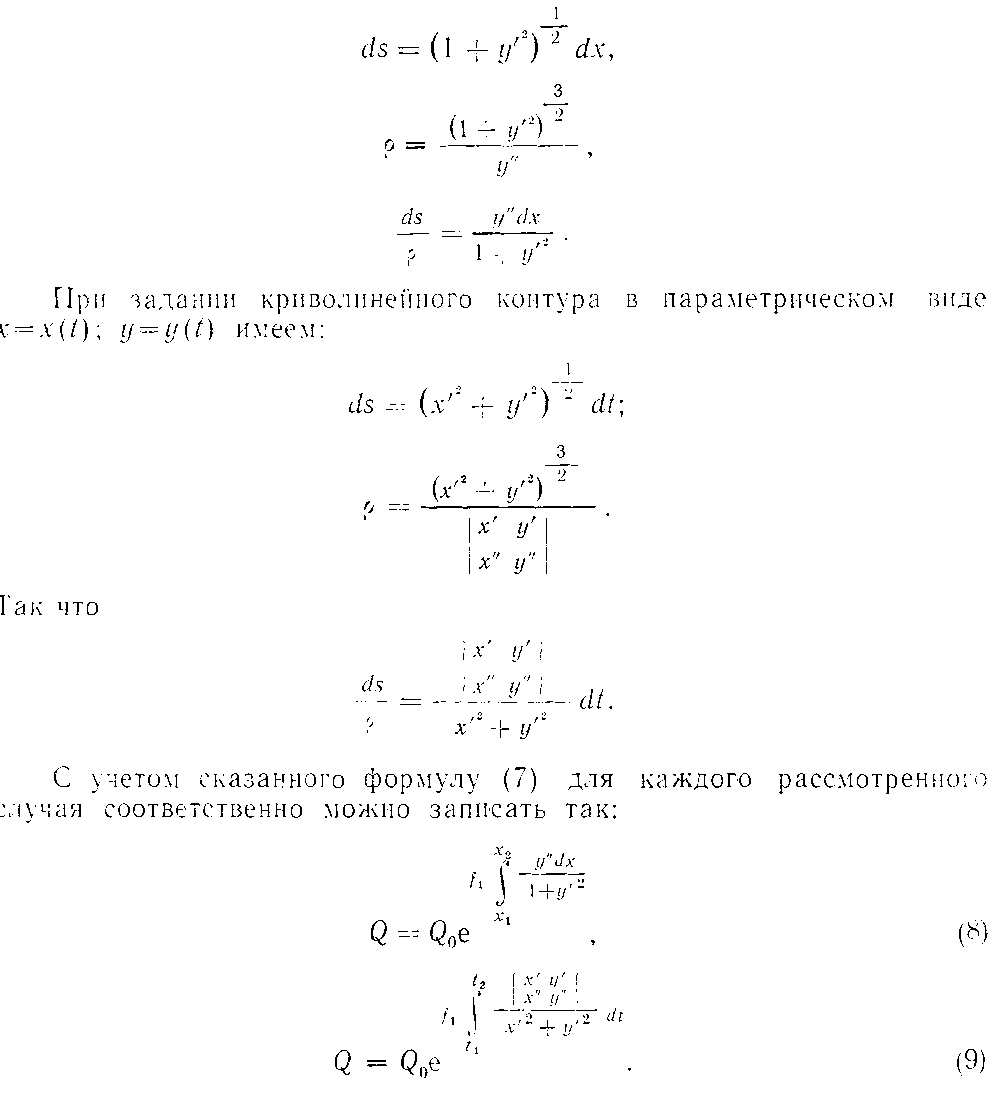ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРОЕКТИРОВАНИЯ НИТЕПРОВОДЯЩИХ УСТРОЙСТВ В ВЯЗАЛЬНЫХ АППАРАТАХ СЕЛЬСКОХОЗЯЙСТВЕННЫХ МАШИН
Э. А. СУХАРЕВ
Среди большого многообразия техники, используемой в сельском хозяйстве, значительную группу составляют машины, оборудованные вязальными аппаратами. К ним относятся льно- и коноплеуборочные, пресс-подборщики, матовязальные, жатки-сноповязалки, табакопришивные и машины для подвязки кустов винограда.
В ближайшие годы планируется значительно увеличить выпуск более производительных, скоростных и надежных машин подобного рода. Чтобы успешно выполнить эту задачу, необходимо разработать новые методы проектирования машин, основанные на глубоком теоретическом анализе и экспериментальной проверке.
В настоящей статье излагается материал, полученный нами в результате разработки единого метода расчета и проектирования нитенаправляющих и нитенатяжных устройств, применяемых в вязальных аппаратах сельскохозяйственных машин.
ОБЩИЙ СЛУЧАЙ ПЛОСКОГО ДВИЖЕНИЯ ГИБКИХ НИТЕЙ
Рассмотрим общий случай плоского движения весомой гибкой или по криволинейным контурам при одновременном действии сжимающих сил, направленных перпендикулярно движению нити и создаваемых с помощью ториевых фланцев.
Будем считать, что исследуемая гибкая нить обладает следующими свойствами: 1) под действием внешних сил принимает любую форму; 2) не сопротивляется изгибу и кручению.
Для вычисления сил трения воспользуемся обобщенным законом Кулона в виде:
![]() (1) где Т сила трения;
(1) где Т сила трения;
f — коэффициент трения;
N - нормальная нагрузка на контакт;
k - коэффициент пропорциональности;
λ—отношение фактической площади контакта к контурной площади;
b - ширина контурной площади;
X -длина контурной площади.
Расчетная схема для решения поставленной задачи приведена на рис. 1.
Движение нити происходит с некоторой скоростью v по плоскому неподвижному контуру cd переменной кривизны, расположенному в вертикальной плоскости XOY, на участке ab в направлении от точки а к b. Одновременно нить на участке ab подвергается действию сжимающих сил интенсивностью p(s), направленных перпендикулярно движению нити вдоль оси OZ. Равнодействующая этих сил равна Р. Скольжение нити но контуру осуществляется под действием концевых натяжений Q, так что
Выделим на участке ab бесконечно малый элемент нити ds с центральным углом da и радиусом кривизны р (рис. 2). В середине элемента поместим натуральный трехгранник с осями β, τ и ν. Причем ось β совпадает с нормалью к дуге ds, ось τ— с касательной к этой дуге, а ось ν перпендикулярна к первым двум осям и параллельна оси ΟΖ.
Пусть ось τ образует с осью ОХ угол Θ. Тогда касательные, проведенные к крайним точкам элемента ds, образуют с осью ОХ соответственно углы![]()
При этом будет выполняться очевидное равенство
Индексы у параметров f, к, λ, b указывают на их отношение к одной из следующих поверхностей трения: 1 — к криволинейному контуру, 2 и 3 — к поверхностям торцевых фланцев.
Рассматривая равновесие элемента нити, спроектируем все силы, действующие на пего, на оси натурального трехгранника.


Применив формулу (7), можно исследовать движение невесомой гибкой нити по любым криволинейным контурам при наличии амонтонова трения.
Выражение, стоящее под знаком интеграла, может быть представлено различным образом. Так, если криволинейный контур, по которому движется нить, задан в декартовых координатах в явном виде y=f(x), то