111.4. ПРОПУСКАНИЕ СОЛНЕЧНОЙ РАДИАЦИИ КРОНОЙ ВИНОГРАДА
Какова бы ни была величина поступающей солнечной радиации, распределение ее внутри кроны будет зависеть от характеристики пропускания солнечных лучей фитомассой. Коэффициент пропускания солнечной радиации ат определяется как отношение [361]:
at = qi/Q1,
где qi — нисходящий поток суммарной радиации внутри кроны для г-того уровня; Q\ — приход радиации на горизонтальную поверхность.
Величина ат отдельного слоя вычисляется как среднее арифметическое:
![]()
где aTi, aTt, ат—коэффициенты пропускания в отдельных точках маршрута; и— число точек.
В табл. 10 в качестве примера приведены значения аГи для сорта Шабаш на вертикальной шпалере. Значения q„ в таблице не приводятся, так как они показаны на рис. 21.
Таблица 10
Коэффициенты пропускания ИР по ярусам кроны винограда на вертикальной шпалере (24 июля 1969 г.)
| Часы | ||||
Ярус |
| 10 | 13 | 16 | 19 |
кроны | поступление ИР на | верхнюю часть | кроны, кал/(см2.мин) | ||
| 0,242 | 0,857 | 1,022 | 0,578 | 0,137 |
Верхний Средний Нижний | 0,44 0,51 0,20 | 0,19 0,17 0,15 | 0,18 0,13 0,10 | 0,26 0,28 | 0,71 0,51 0,35 |
В утренние и вечерние часы коэффициенты пропускания довольно высокие. Однако надо принять во внимание, что в эти часы величина ат обусловливается главным образом радиацией, проникающей через боковые стороны кроны. По мере приближения к полуденным часам значения коэффициентов резко уменьшаются.
Коэффициенты пропускания, подобные представленным в табл. 10, позволяют получить радиационные характеристики дайной конкретной кроны, т. с. они имеют локальный характер. Более универсальной характеристикой ат является функция aT = f (LAI). В этом случае по значению LAI для данной культуры, независимо от места и времени проведения работы, может быть рассчитана величина ат или же решена обратная задача: найдена величина ILAI, которая с учетом поступления радиации и величины ат обеспечивала бы в том или ином участке кроны интенсивность радиации, достаточную для высокой фотосинтетической активности листьев.

Рис. 18. Зависимость функции пропускания суммарной ИР aTa от относительной площади листьев кроны винограда в течение дня. Сорта: 1 — Ркацители, 2 — Шабаш, 3 — Рислинг рейнский,
На рис. 18 показаны полученные нами экспериментально зависимости aTa = f (ILAIC) кроны куста в разные часы дня. Увеличению ILAIr соответствует понижение уровня пиранометра в кроне. При шести уровнях высоты кроны и восьми сериях для каждого срока получено 48 точек, характеризующих эту связь. В широком диапазоне дневных часов между аГи и ILAIr обнаруживаются тесные обратные линейные связи. Числовые характеристики уравнений приведены в табл. 11.
Таблица 11
Уравнения связи ajJILAIr и атф/ИА1г для кроны виноградного куста в разные часы дня (август)

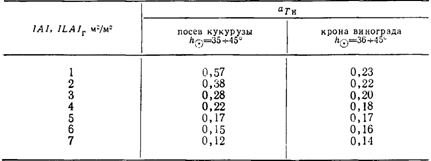
Представляло интерес сопоставить характер ослабления радиации фитомассой винограда при рядовой посадке с растительностью, имеющей сплошной покров. Из табл. 12 видно, что при LAl=\ величина ату кукурузы [366] более чем вдвое больше, чем у винограда при /JL4/r=l. При увеличении листового индекса до 2 разница сокращается, и при LAI = 3-г-7 значения am оказываются близкими. Относительно низкие аТа у винограда при малых ILAIr можно объяснить особенностями структуры верхнего слоя кроны, где часть побегов после окончания роста подвязывается к верхней проволоке горизонтально и в результате создается как бы эффект «экранирования».
Таблица 12
Изменение aja в зависимости от величины LAI посева кукурузы [366] и ILAIr кроны винограда
Как известно, в фитоценозах со сплошным покровом зависимость ослабления солнечной радиации от относительной площади листьев имеет вид экспоненты [306, 360]. Вместе с тем анализ экспериментальных данных показывает (рис. 19), что функцию aTn=f(LAI) можно удовлетворительно аппроксимировать при помощи двух прямолинейных отрезков: в интервале 1.Л1 = 0+2, где ослабление радиации наибольшее, и в интервале £Л/ = 2ч-7, где ослабление радиации происходит значительно слабее. Для винограда функции aTJILAIr и aT$/ILAIr для отдельных часов дня получены в интервале ILAlr = 2~l3, т. е. они приближаются ко второму участку экспоненты функции ати/LAl для ценозов сплошного покрова.
Аппроксимация криволинейных функций отрезками прямой имеет место и в других случаях. Отмечается, в частности, что предложенная Е. Рабиновичем (цит. по [360]) формула зависимости функции фотосинтеза от плотности потока падающей ФАР аппроксимирует световую кривую фотосинтеза также при помощи двух прямолинейных отрезков.
Как известно, радиационное поле внутри РП вследствие изменения соотношения между ФАР и БИКР 1 характеризуется неопределенностью состава суммарной ИР. Для перехода от коэффициентов пропускания ИР am к приближенным значениям коэффициентов пропускания ФАР атф Тоомингом [360] вычислены переходные коэффициенты (табл. 13). При /tc,>20° переход от аТи к атф не зависит от h.

Рис. 19. Зависимость функции пропускания суммарной IIP от относительной площади листьев в посевах кукурузы. а — пасмурно; б — ясно:

Расчеты показали, что зависимость пропускания ФАР от относительной площади листьев кроны винограда и времени дня представляется графически семейством параболических кривых, асимметричных по отношению к полдню (рис. 20). Эти кривые могут быть описаны математически.
1 БИКР — близкая инфракрасная радиация.

Рис. 20. Зависимость функции пропускания ФАР кроной винограда от времени дня т при разных значениях относительной площади листьев ILAIr.
Как известно, для характеристики радиационных потоков внутри посевов со сплошным покровом в зависимости от площади листьев (или индекса LAI) предложены различные математические модели, отражающие закономерности ослабления солнечной радиации внутри РП [100, 247, 365, 411, 471, 478,506].
Отмечая сложность теоретических формул и их приближенность, Росс и Тооминг [306, 360] предложили для описания режима солнечной радиации в посевах ряд полуэмпирических формул, в которых теоретические функции заменены эмпирическими постоянными.
Для количественного описания зависимости пропускания ФАР от ILAIr кроны винограда по экспериментальным значениям ити для отдельных часов дня с помощью переходных коэффициентов (табл. 13) были вычислены приближенные значения аТф для соответствующих значений lLAIr и часов дня т и по ним рассчитаны регрессионные связи атъ/ILAIr (см. табл. 11).
Последующая обработка данных, выполненная с помощью ЭВМ Мир-1, показала, что функция аТф = 1(ILAIr, т) для кроны винограда хорошо аппроксимируется полиномом пятой степени вида

где ILAIr — относительная площадь листьев кроны; т — целые часы времени между восходом и заходом Солнца; At, Bi (i= = 0-:-5) — постоянные коэффициенты:

Расписывая формулу в виде

Применение формулы ограничивается условием, когда ширина кроны куста составляет 40—60 см, a /Li4/B = 3-r-5.